Introduction
There is a lot of literature about CRC. May be too much. Because CRC is, in essence, a very simple concept. Not much more complicated than a division with remainder. Probably the main problem is, that CRC is both a mathematical concept and a technical, hardware or software driven implementation.
The mathematical point of view is that CRC is a small, unimportant sector of a galaxy called “Algebraic Coding Theory”. Mathematicians aren't much interested in technically “good” codes, since these have already been discovered and analyzed long ago. So don't expect much help from mathematicians (except for me, of course). Mathematically “interesting” codes may have poor data rates (ratio between “net” data and overhead required for redundancy), which make them uninteresting for technical use. On the other side, computer oriented people seem to feel little challenge on fully understanding the math behind the CRC. They just want to have their algorithm working.
The CRC++ Project
There is a CRC reference implementation on the net which helped for many purposes. But this implementation also created a couple of problems, because people tend to use available implementations without fully understanding them.
When trying to understand CRC, the main concept to grab is that data is not represented as integer numbers, but as coefficients of a polynomial. Since most computer hardware has been designed to crunch numbers, not polynomials, a little bit of hand work is required, which makes the computation slightly more complicated than integer division. Again, a lot of stuff has been published on that matter.
One important fact to note is that there is not just one way to represent (binary) polynomials in a computer. Take a look at the eight bits of a byte. Each of them represent a coefficient. But which one?
There are in fact two good choices. One which I call
“native”, where the meaning of a bit with the binary value
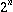 is the coefficient of
is the coefficient of 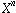 . This is the representation used in Ross Williams
reference implementation. The other is called representation in
“network” order. Network order applies to network
applications, where data is transmitted serially, bit by bit, over a wire
or other media. When transmitting a polynomial via serial communications,
the highest coefficient is always transmitted first, in order to make CRC
computation feasible with simple electronic devices like shift registers.
Therefore, in serial communications, the meaning of a bit depends on the
transmission order, which is usually least significant bit (LSB) to most
significant bit (MSB).
. This is the representation used in Ross Williams
reference implementation. The other is called representation in
“network” order. Network order applies to network
applications, where data is transmitted serially, bit by bit, over a wire
or other media. When transmitting a polynomial via serial communications,
the highest coefficient is always transmitted first, in order to make CRC
computation feasible with simple electronic devices like shift registers.
Therefore, in serial communications, the meaning of a bit depends on the
transmission order, which is usually least significant bit (LSB) to most
significant bit (MSB).
The consequence is, that in “network” bit order, the
LSB bears the highest polynomial coefficient and the MSB bears the lowest
coefficient. This is just the opposite of the “native” order.
In order to accomodate for network order, Ross Williams' reference
implementation introduces the notion of “reflected” data
and/or result polynomial (parameters
“refin”/“refout”).
However, the reference implementation provides a number of parameters
which cannot be chosen at random, and this is which might make the correct
selection of the parameters difficult.
CRC++ Concepts
The approach of CRC++ is to have separate classes for each
polynomial representation. This makes the notion of reflected data
obsolete. To use CRC++, you have to choose a polynomial and a data
representation. You should be aware that a polynomial is a mathematical
object, and that its computer representation is given in one of the two
orders described above. For example, the CCITT polynomial is
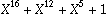 , which translates to
, which translates to 0x1021 in
native order, and to 0x8408 in network order[1].
To be compatible with existing applications, the choice is not free. For example, to be compatible with X.25, HDLC/SDLC, or Ethernet, you must chose network order representation.
CRC++ is entirely based on C++ templates. It is compatible with any modern C++ compiler.
Besides the raw mathematics of the calculation, most CRC usages
include some “folkloristic” additions, like providing a
preset value and/or inverting the computed CRC before transmission. In
CRC++, the raw calculations are done in a CRC<>
template class, and the folkloristik additions are implemented in a
CRCStream<> template class.
Further reading
-
Please have a look at the “Never Asked Questions” list.
-
The sources of CRC++ are now available at GitHub.
-
Ross William's CRC Pitstop. Includes the famous reference implementation.
-
Richard Blacks article on Fast CRC32 in Software. Contains a good introduction to the underlying math.
-
The ITU-T Recommendation X.25 describes CRC-CCITT in detail. The PDF version is now available free of charge.
[1] This notation assumes that the highest coefficient is not represented explicitely, because it is known to be always 1. There exist other notations which make use of the fact that the lowest coefficient must also always be 1, and can therefore also be suppressed. This leads to a different binary/hexadecimal notation.