These are CRC Guru's answers to the questions you never dared to ask.
The Never Asked Questions
| Q: | CRC means Cyclic Redundancy Check. But what does that mean? |
| A: | The word “cyclic” means that it is based on cyclic codes. “Redundancy” means that something is added to your data which does not increase the amount of information. |
| Q: | What is a code in general and a cyclic code in particular? |
| A: | A code is a set of words of an alphabet
F of symbols. A block code
is a code where each word has a fixed length n.
Block codes have the property that there is number
d, called the minimum distance, such that any
two words of the code differ at least in d
places. This property can be used for error detection and
correction: if a code has minimum distance d, then either
d-1 errors can be detected, or
[(d-1)/2] errors can be corrected. A
cyclic code is a block code for which any
shift of a valid code word is also a valid code word. Cyclic codes
can be described with polynomials[1], and in this description they have the property that
any code word can be expressed as a multiple of a certain
polynomial, called the generator polynomial.
The codes we are dealing with here are based on an alphabet of two
symbols, ordinary referred to as bits.One thing to remark here is that the data which is processed
by a CRC algorithm always has a fixed length, the block length
|
| Q: | Does a CRC polynomial have to be irreducible? |
| A: | No. In fact, some popular CRC polynomials are divisible by X+1.[3] |
| Q: | Can I choose a CRC polynomial at random? |
| A: | No. The polynomial is required to divide 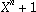 , where n is the block
length of the cyclic code. |
| Q: | The Polynomial for CRC-CCITT/XModem is mostly referred to as
0x1021. But there are also references which
say, it is 0x8408. Which one is correct? |
| A: | If interpreted in the right way, both. The CCITT polynomial
is 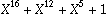 , which translates to
0x1021 or to 0x8408,
depending on the bit
order chosen. However, it does not make any sense to
interpret a bit pattern as a polynomial without specifying the bit
order. Therefore, the Catalog
of Parameter Sets for Standards which is part of the
Painless
Guide to CRC Error Detection has certainly a flaw in this
point. |
| Q: | What is the correct byte order for transmitting the computed CRC? |
| A: | Do not attempt to interpret the computed CRC as an integer value. It is a polynomial. So the correct answer is that the byte containing the highest coefficient of the computed polynomial must be transmitted first. When using Ross Williams' reference implementation, this corresponds to the low order byte when “reflection” is used, and to the high order byte when reflection is not used. In CRC++, the result() method automatically delivers the result in a byte order suitable for insertion into the output stream. |
| Q: | What is a residual value? |
| A: | Some CRC variations invert the result before transmission.
In a straightforward implementation, a correct block would then
yield a result of L(X), the all-ones-polynomial[4]. However, all CRC algorithms require that the input
data stream is multiplied by 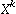 , where k is the degree of the CRC
polynomial. If the same algorithm is used for verification, then
the result for a correct block is not L(X), but the remainder of
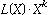 . This value is called the residual. It is
constant for a given CRC polynomial. In CRC++, the good() method takes care of
comparing against the correct value, so you don't have to deal
with it. |
[1] To be precise: a polynomial algebra, in which all
calculations are done modulo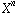 
, where n is the
block length.
[2] The block size for CRC-CCITT and for CRC-16 is
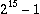bits, but for CRC-32 the block size is
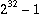bits.
[3] For example, the CCITT-16/XModem polynomial
= 
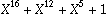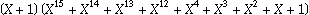
The CRC-16 Polynomial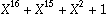 
= 
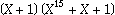
[4] This notation has been taken from Richard Black's article on Fast CRC32 in Software.